Simulated Annealing

Annealing

Annealing is the process of heating and then cooling a substance is a controlled way. After a solid substance has been heated beyond is fusion point, the properties of this substance depend on the cooling rate. If the substance is gradually cooled down, the result is a strong crystalline structure. If the substance is quickly cooled down, the result is a defective fragile structure.
El templado es el proceso de calentar y después enfriar una sustancia en forma controlada. Después de que una sustancia sólida se ha calendado más allá de su punto de fusión, las propiedades de ésta sustancia dependen de la razón de enfriamiento. Si la temperatura desciende en forma gradual y controlada, el resultado es una estructura cristalina fuerte. Si la sustancia se enfría rápidamente, el resultado es una estructura defectuosa quebradiza.

Simulated Annealing

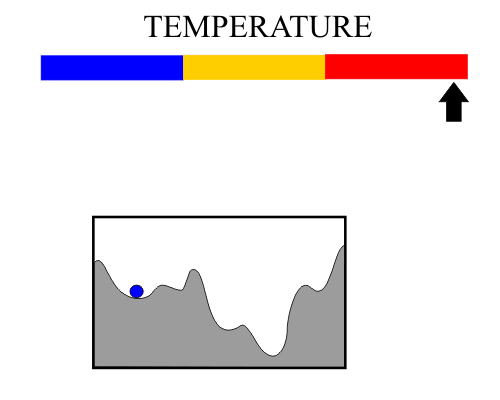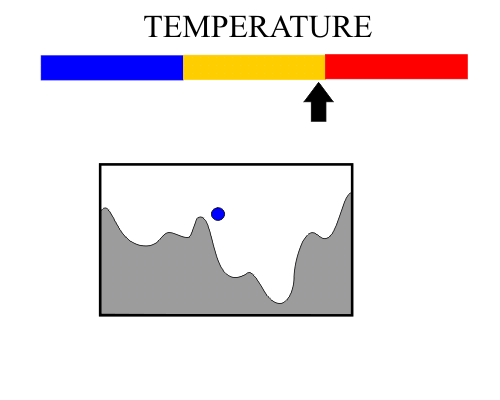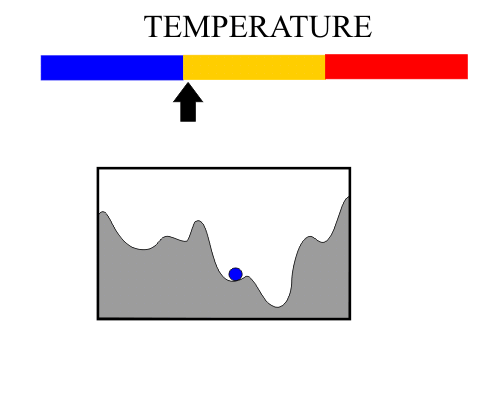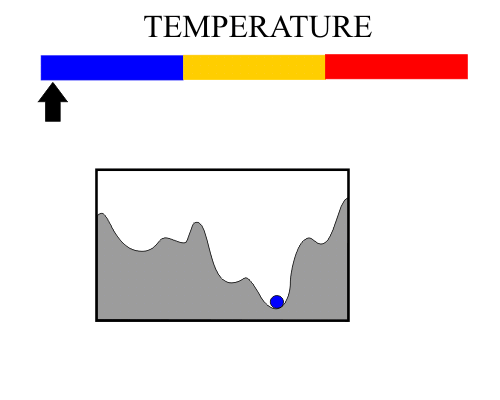
Simulated annealing is an optimization method that mimics the process of annealing. The figure shown below illustrates the basic operation of simulated annealing. At the beginning the temperature is high and the ball has enough energy to move and jump high peaks, as temperature decreases the energy of the ball allow it to move lightly itself. In this case, at the end of the simulation the ball must be in a state of minimum energy.
El templado simulado es un método de optimización que imita el proceso de templado. La figura de abajo muestra el principio básico de operación del templado simulado. Al principio, la temperatura es alta y la pelota tiene suficiente energía para moverse y saltar picos altos, a medida que la temperatura disminuye la energía de la pelota le permite moverse solo ligeramente. En este caso, al final de la simulación la pelota debe encontrarse en un estado de mínima energía.

BasicOperation

Tip
It can be said that the red region (high temperature) is a time for exploring. In the same way, we can say that the yellow region (medium temperature) is a time for drafting the solution. Finally, the blue region (low temperature) is a step to improve the solution.
Se puede decir que la región roja (alta temperatura) es un tiempo de exploración. En la misma forma se puede decir que la región amarilla (temperatura medias) es bosqueja la solución. Finalmente, la región azul (baja temperatura) es una etapa para mejorar la solución.

Cooling Types

The way a substance is cool down is called cooling schedule. There are two typical cooling schedules: linear and exponential.
La forma en que una sustancia se enfría se llama calendario de enfriamiento. Hay dos calendarios típicos de enfriamiento: lineal y exponencial.

Linear Cooling

The figure below shows how linear cooling is performed. At the beginning of the simulation, T1 is set to the initial temperature value. The temperature remains constant for some period of time Δ, and then the temperature is reduced using the equation shown. The constants a and b are real values, and determine the cooling schedule.
La figura de abajo muestra cómo opera el enfriamiento lineal. Al inicio de la simulación, T1 es fijada en un valor inicial de temperatura. La temperatura permanece constante por periodo de tiempo Δ, y entonces la temperatura se reduce usando la ecuación mostrada. Las constantes a y b son valores reales y determinan el calendario de enfriamiento.

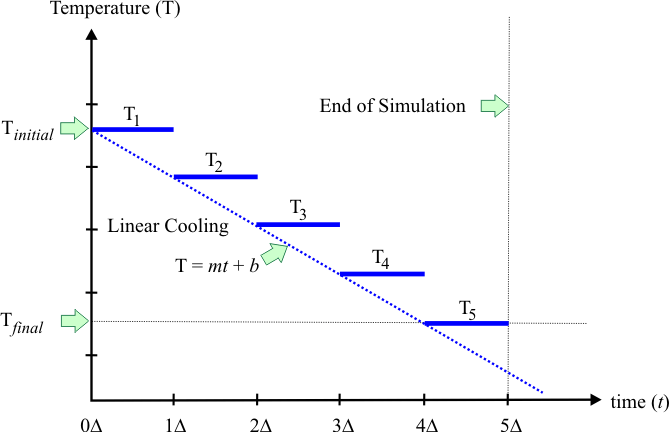
LinearCooling

Problem 1
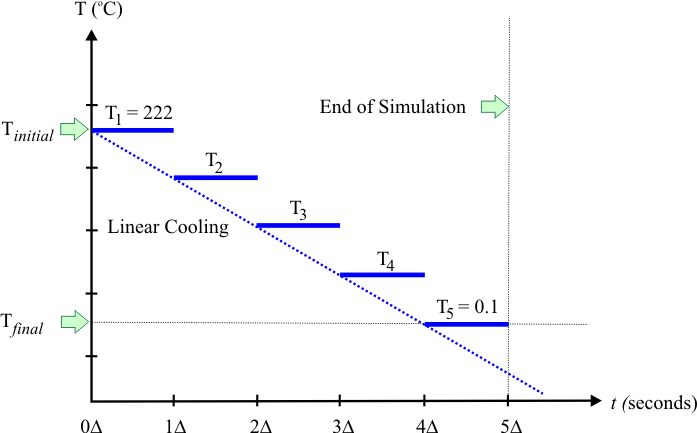
Show that in linear cooling, when there are N temperatures, the temperature is given by:
Demuestre que en un enfriamiento lineal, cuando hay N temperaturas, la temperatura está dada por:

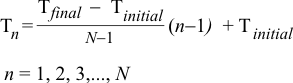
LinearCoolingFormula

Problem 2
A professor is performing simulated annealing with a linear cooling schedule for teaching purposes. If the initial temperature is 222 o C, and the final temperature is 0.1 o C, (a) What are the values of T2, T3 and T4? (b) Check that the value of T5 is 0.1. You may use Microsoft Excel.
Un profesor está realizando templado simulado con enfriamiento lineal para propósitos de enseñanza. Si la temperatura inicial es 222oC, y la temperatura final es de 0.1oC, (a) Cuales son los valores de T2, T3 y T4? (b) Verifique que el valor de T5 sea 0.1oC. Usted puede usar Microsoft Excel.

LinearCoolingExe

Exponential Cooling

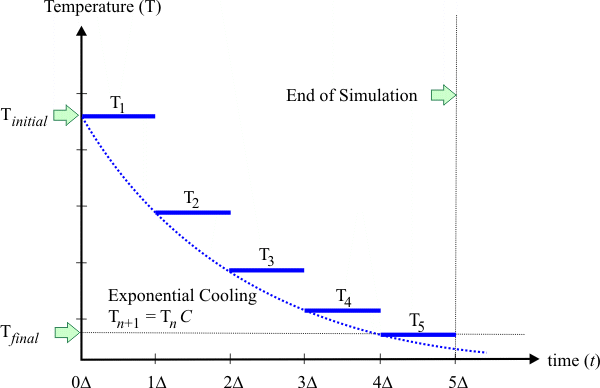
The figure below shows how exponential cooling is performed. At the beginning of the simulation, the value of T1 is set to the value of the initial temperature. The temperature remains constant for some period of time Δ. Then the value of T2 is computed as the product of T1 times C, where C is a constant with a value less than one.
La figura de abajo muestra cómo opera el enfriamiento exponencial. Al principio de la simulación el valor de T1 se fija al valor de la temperatura inicial. La temperatura permanece constante por un periodo de tiempo Δ. Entonces el valor de T2 se calcula como el producto de T1 con C, donde C es una constante con valor menor a uno.

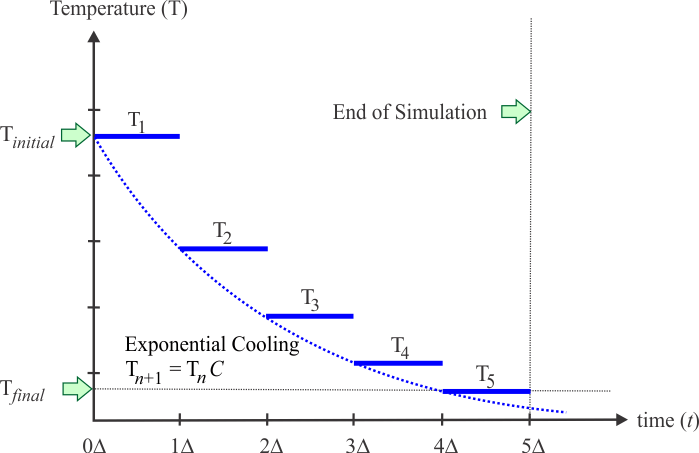
ExponentialCooling

Problem 3
Compare how much time the simulation spends at high temperatures versus the time the simulation spends at low temperatures: (a) When a liner cooling schedule is used, (b) When an exponential cooling schedule is used.
Compare cuanto tiempo pasa la simulación a altas temperaturas contra el tiempo que la simulación pasa a bajas temperaturas: (a) Cuando la tasa de enfriamiento es lineal, (b) Cuando la tasa de enfriamiento es exponencial.

Problem 4
Based on your answer in the previous problem: (a) When a linear cooling schedule should be used?, (b) When an exponential cooling schedule should be used?
Basado en su respuesta del problema previo: (a) Cuándo se debería de usar una tasa de enfriamiento lineal?, (b) Cuándo se debería de usar una tasa de enfriamiento exponencial?

Problem 5
Show that in exponential cooling, when there are N temperatures, the constant C is given by:
Demostrar que el enfriamiento exponencial, cuando hay N temperaturas, la constante C está dada por:

ExponentialCoolingFormula

Tip
An analogy with the cooling process consists in looking for the deepest whole over the earth surface. Thus, when using an exponential cooling schedule, at high temperatures, the search is performed by airplane, while at low temperatures the search is performed by foot.
Una analogía con el proceso de enfriamiento consistiría en buscar el agujero más profundo sobre la superficie de la tierra. Así en el enfriamiento exponencial, a altas temperaturas la búsqueda se realiza en avión, mientras que a bajas temperaturas la búsqueda se realiza a pie.

Problem 6
A student is performing simulated annealing for a class project. If the initial temperature is 333o C, the final temperature is 0.001o C, and there are five temperatures as shown below. (a) What are the values of T2, T3 and T4? (b) Check that the value of T5 is 0.001. You may use Microsoft Excel.
Un estudiante está realizando simulated annealing para un proyecto de clase. Si la temperatura final es 333o C, la temperatura final es 0.001o C, y hay cinco temperaturas cómo se muestra debajo. (a) Cuales son lo valores de T2, T3 and T4? (b) Verifique que el valor de T5 es 0.001. Usted puede usar Microsoft Excel.

ExponentialCoolingExe

Simulated Annealing Requirements

In order to use simulated annealing to solve a problem, there are four requirements that the problem must meet:
  1. Solution coding. The solution of the problem can be expressed as a set of variables
  2. Initialization. It is possible to create an initial solution for the problem (the solution does not need to be optimal)
  3. Perturbation. It is possible to perturb (alter) a solution to create a new one
  4. Error Evaluation. It is possible to compute a real value called error to indicate the quality of a solution
A fin de usar el templado simulado para resolver un problema, hay cuatro requisitos que el problema debe cumplir:
  1. Codificación de la solución. La solución del problema se puede expresar como un conjunto de variables
  2. Inicialización. Es posible crear una solución inicial para el problema (la solución no necesita ser óptima)
  3. Perturbación. Es posible perturbar (alterar) una solución para crear una nueva
  4. Evaluación del Error. Es posible calcular un valor real llamado error que indique la calidad de una solución

Tip
In order to perform the Error Evaluation, an error function must be defined. To improve the performance of SA, it is very important that this function does not exhibit discontinuities.
A fin de realizar la Evaluación del Error, una función de error debe ser definida. Para mejorar el desempeño de SA, es muy importante que esta función no exhiba discontinuidades.

Iterations

At each temperature the algorithm spends some time while performing a specified number of iterations. Each iteration has two steps:
  1. Perturbation. A new solution is created by randomly perturbing the current solution.
  2. Error Evaluation. The new solution is evaluated to find out if it is better than the previous one.
A cada temperatura el algoritmo permanece cierto tiempo mientras realiza un número específico de iteraciones. Cada iteración tiene dos pasos:
  1. Perturbación. Una nueva solución es creada perturbando en forma aleatoria la solución actual.
  2. Evaluación del Error. La nueva solución es evaluada para averiguar si es mejor que la solución previa.

Probability of Acceptance

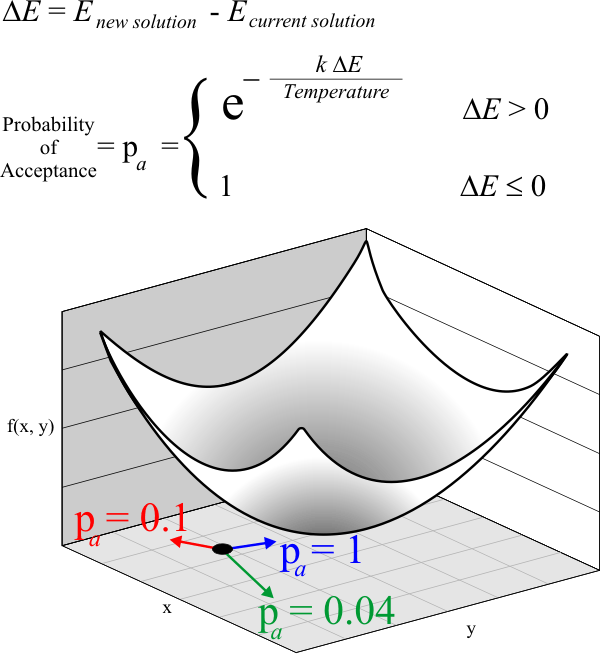
Once a solution has been perturbed, the new solution must be evaluated. Simulated Annealing may replace the current solution with the new solution with certain probability called probability of acceptance. The equation below shows how the probability of acceptance is computed. The set of equations below are known as the Metropolis algorithm in honor of Metropolis. Where K is a constant that needs to be determined.
Una vez que una solución ha sido perturbada, la nueva solución debe ser evaluada. El templado simulado puede reemplazar la solución actual con la nueva solución con una cierta probabilidad llamada probabilidad de aceptación. La ecuación de abajo muestra como se calcula la probabilidad de aceptación. El conjunto de ecuaciones de abajo son conocidas como el algoritmo de Metropolis en honor de Metropolis. Donde K es una constante que necesita determinarse.

Metropolis

Tip
The Metropolis algorithm may be easily implemented in any programming language. The function below shows the implementation in the C++ language using the library tr1 to generate random numbers (in most recent compilers, most elements of tr1 are part of the C++ standard). You may use any other library or function to generate random numbers. The function returns true when the new solution must be accepted.
El algoritmo de Metropolis puede ser fácilmente implementado en cualquier lenguaje de programación. La función de abajo muestra la implementación en el lenguaje C++ usando la librería tr1 para generar números aleatorios (en compiladores recientes, la mayoría de los elementos de tr1 son parte ahora del C++ estandar). Usted puede usar otra librería u otra función para generar números aleatorios. La función regresa true cuando la nueva solución es aceptada.

SimulatedAnnealing.cpp
bool SimulateAnnelaing::Accept(double currentError, double newError, double temperature)
{
     //std::tr1::default_random_engine random_generator;
     std::default_random_engine random_generator;

     //std::tr1::uniform_real<double> dist(0.0, 1.0);
     std::uniform_real<double> dist(0.0, 1.0);

     double deltaError = newError - currentError;
     if (deltaError < 0) return true; //Accept the solution, if the solution improves

     //Accept the solution with a given probability
     if (dist(random_generator) < exp(-k*deltaError/temperature)) return true;
     return false;
}


Problem 7
A computer is performing simulated annealing. At the beginning of an iteration, the current solution had an mse of 0.5. When the current solution was perturbed, the mse of the new solution was 0.49. Suppose that k is 100.56. Compute the probability of acceptance, if the temperature is: (a) 100, (b) 10, (c) 1.
Una computadora se encuentra realizando templado simulado. Al principio de una iteración, la solución actual tenía un mse de 0.5. Cuando la solución actual fue perturbada, el mse de la nueva solución fue 0.49. Suponga que k es de 100.56. Calcule la probabilidad de aceptación, si la temperatura es de: (a) 100, (b) 10, (c) 1.

Problem 8
A student is performing simulated annealing. At the beginning of an iteration, the current solution had an mse of 0.8. When the current solution was perturbed, the mse of the new solution was 0.805. Suppose that k is 8.72. Compute the probability of acceptance, if the temperature is: (a) 100, (b) 10, (c) 0.001. (d) When is the probability of acceptance higher, at high or low temperatures?
Un estudiante se encuentra realizando templado simulado. Al principio de una iteración, la solución actual tenía un mse de 0.8. Cuando la solución actual fue perturbada, el mse de la nueva solución fue de 0.805. Suponga que k es de 8.72. Calcule la probabilidad de aceptación, si la temperatura es de: (a) 100, (b) 10, (c) 0.001. (d) Cuando es la probabilidad de aceptación más grande?, a altas o a bajas temperaturas?

Tip
Simulated Annealing can be seen as a three step process as the temperature decreases:
  • Exploring for a solution (high temperatures)
  • Drafting a solution (medium temperatures)
  • Improving a solution (low temperatures)
El Templado Simulado puede verse con un proceso de tres pasos cuando la temperatura disminuye:
  • Explorar buscando una solución (altas temperaturas)
  • Bosquejar una solución (temperaturas medias)
  • Mejorar una solución (bajas temperaturas)

Problem 9
One of the main problems of using Simulated Annealing is to know the proper value k in the Metropolis algorithm. This value of k can be estimated before SA starts. One simple way to estimate k is by creating a random solution and perturb it a number of times M. For each perturbed solution, there is an associated error Ei that can be calculated. Thus, there is a set of error: E1, E2, ..., EM. If ΔE can be estimated as the sample standard deviation of the errors, and if the probability of acceptance must be 0.05 at the beginning of the simulation, show that k can be estimated as follows.
Uno de los principales problemas de usar el templado simulado es conocer el valor apropiado de k en el algoritmo de Metropolis. Esta k puede estimarse antes de comenzar el SA. Una forma simple de estimar k es creando una solución aleatoria y perturbarla un número de veces M. Para cada solución perturbada, hay un error asociado Ei que puede ser calculado. Así, hay un conjunto de errores: E1, E2, ..., EM. Si ΔE puede ser estimado como las desviación estándar de una muestra de los errores, y si la probabilidad de aceptación debe ser de 0.05 al principio de la simulación, demuestre que k puede ser estimada como sigue.

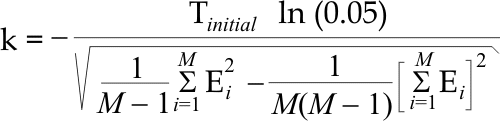
EstimateK

Problem 10
A student created a random initial solution. Then, he perturbed this solution several times. The respective errors for each solution were: 0.5, 0.55, 0.52, 0.51, 0.502, 0.56, 0.6, 0.48, 0.52, 0.7. Estimate the value of k for an initial temperature of 222. Suppose that the probability of acceptance must be 0.05 at the beginning of the simulation.
Un estudiante creó una solución inicial aleatoria. Entonces, él perturbo la solución varias veces. Los errores respectivos para cada solución fueron: 0.5, 0.55, 0.52, 0.51, 0.502, 0.56, 0.6, 0.48, 0.52, 0.7. Estimar el valor de k para una temperatura inicial de 222. Suponga que la probabilidad de aceptación debe ser de 0.05 al principio de la simulación.

Simulated Annealing Example

The figure below shows how to use Simulated Annealing to solve a system of equations. The algorithm begins by using random values for x and y. These values are, then, perturbed by adding random values. The mse is computed for each case. When the mse reduces, the perturbed solution becomes the actual solution. The algorithm stop when the mse is less than a specified value.
La figura de abajo muestra cómo usar el Templado Simulado para resolver un sistema de ecuaciones. El algoritmo comienza asignando valores aleatorios a x y y. Estos valores son, entonces, perturbados sumando valores aleatorios. El mse es calculado para cada caso. Cuando el mse se reduce, la solución perturbada se convierte en la solución actual. El algoritmo se detiene cuando el mse es menor que un valor específicado.

SystemOfEquations

Tip
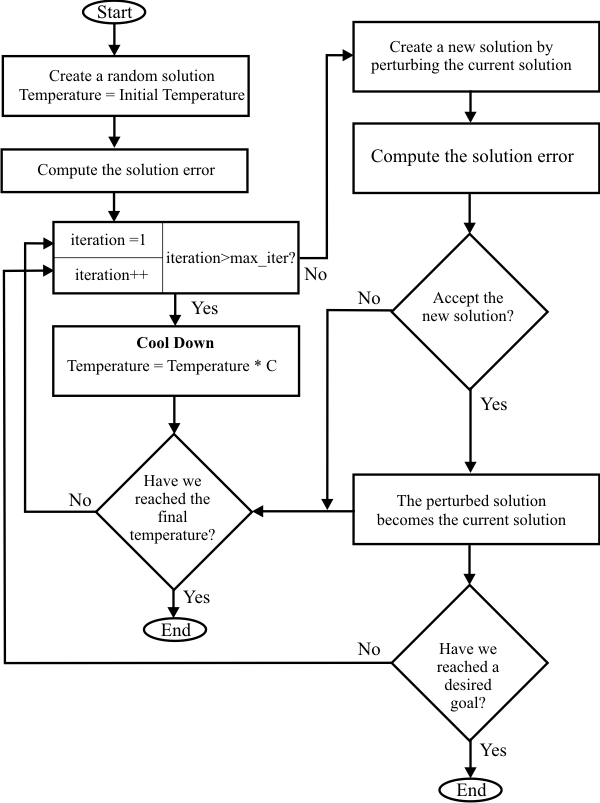
The figure below illustrates the basic operation of simulated annealing. The optimization process begins at the initial temperature, and a random solution is created. Then, the simulation iterates at the same temperature by perturbing the current solution and evaluating the solution error. The Metropolis algorithm is, then, used to accept or reject solution. When the number of iterations is completed, the temperature decreases, and the simulation iterates at a new temperature. The simulation stops when the temperature reaches the final temperature value or when a desired goal is met.
La figura de abajo ilustra la operación básica del templado simulado. El proceso de optimización comienza a la temperatura inicial, y una solución aleatoria es creada. Entonces, la simulación realiza iteraciones a la misma temperatura al perturbar la solución actual y evaluar el error de la solución. El algoritmo de Metropolis es, entonces, usado para aceptar o rechazar una solución. Cuando el número de iteraciones es completado, la temperatura disminuye, y la simulación realiza las iteraciones a una temperatura nueva. La simulación se detiene cuando la temperatura alcanza su valor final o cuando la meta deseada es alcanzada.

BlockDiagram

Function Minimization

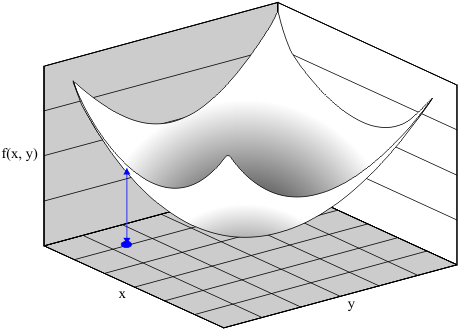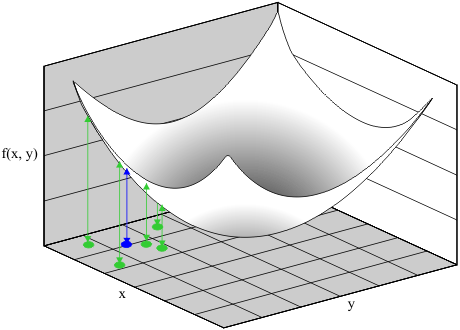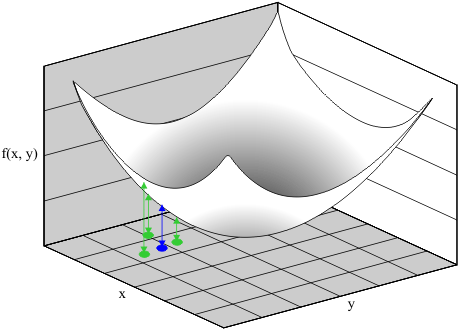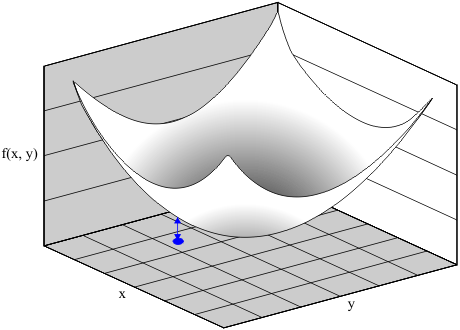
Simulated annealing can be used to find the minimum of a function as illustrated below. The simulation begins with the random solution shown in blue. This solution is perturbed to create new solutions; these are displayed in green. The solution with the smallest error becomes the actual solution. The process repeats itself.
El templado simulado puede ser usado para encontrar el mínimo de una función como se ilustra debajo. La simulación comienza con una solución aleatoria mostrada en azul. Esta solución es perturbada para crear soluciones nuevas, estas son mostradas en verde. La solución que tiene el error más pequeño se convierte en la solución actual. El mismo proceso se repite.

Equation2D

Problem 11
Find the minimum of equation shown below using Simulated Annealing, Microsoft Visual Studio and Wintempla. Create a Simulated Annealing Application called Minimi using Wintempla as shown.
Encuentre el mínimo de la ecuación mostrada debajo usando Templado simulado, Microsoft Visual Studio y Wintempla. Cree una Simulated Annealing Application llamada Minimi usando Wintempla como se muestra.

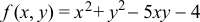
FuncEquation

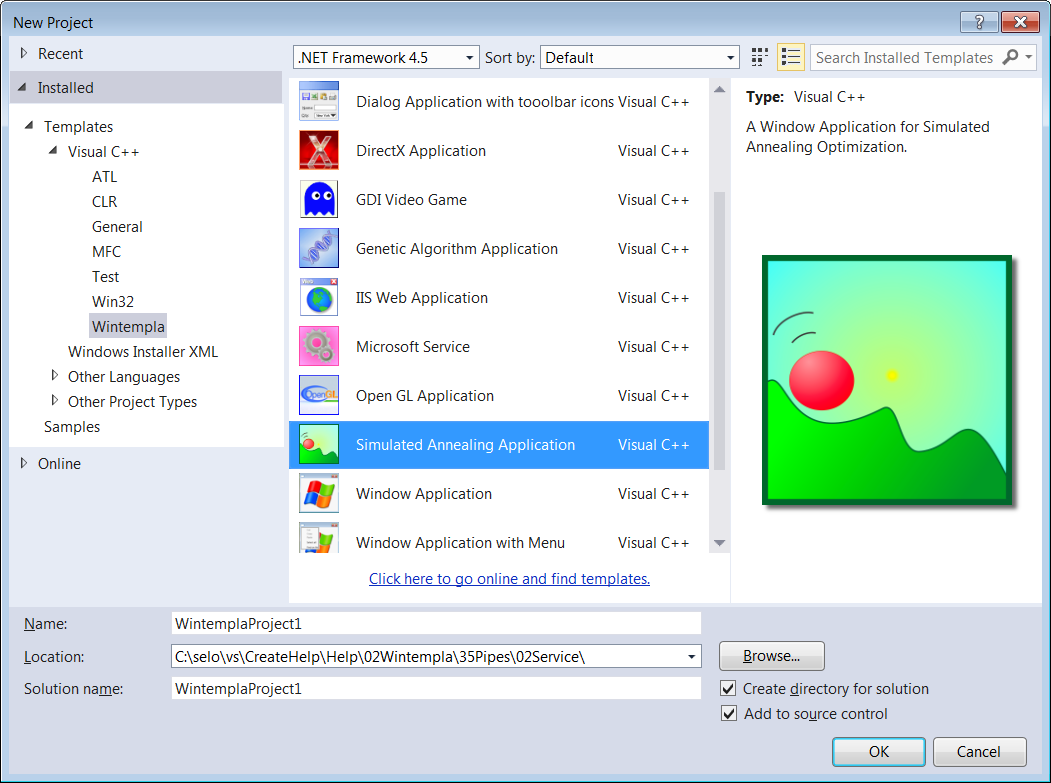
MinimiWizard

Solution 11
Wintempla will generate a multi-thread program with a basic configuration to perform the optimization. You may edit the Solution.h and Solution.cpp files to customize the optimization. The wizard provides some sample code to minimize the equation of the problem; so you not need to edit any code for this example. You must, however, edit these files for other optimization problems. As a matter of fact, you must provide code to perform the following five steps:
  1. Solution coding
  2. Initialization
  3. Perturbation
  4. Error Evaluation
  5. Solution Copy
Wintempla generará un programa multi-tarea con una configuración básica para realizar la optimización. Usted puede editar los archivos Solution.h y Solution.cpp para personalizar la optimización. El asistente proporciona algunos códigos muestra para minimizar la ecuación del problema, así que usted no tiene que editar nada de código para este ejemplo. Usted debe, sin embargo, editar estos archivos para otros problemas de optimización. De hecho, usted debe proporcionar el código para realizar los cinco pasos siguientes:
  1. Codificación de la solución
  2. Inicialización
  3. Perturbación
  4. Evaluación del error
  5. Copiar una solución

Tip
Observe the following key points in the program:
  1. The solution coding is straightforward, one double value is used for x, and another double is used for y
  2. A random value was used to initialize x and y.
  3. The solution was perturbated by adding a random value to x and y
  4. As this is a minimization problem, the function itself can be used to evaluate the function. Thus, it is possible (in this case) to just evaluate the function in order to evaluate the error.
  5. The SimAnnealCopy function copies all the variables that were used in the coding, in this case: x and y.
  6. When the program begins execution, another threat starts to perform the optimization. Thus, there are two threads in this program.
  7. The main window starts a timer that runs a block of code every second.
  8. The timer is used to move information from the optimization thread to the main window thread, so that the user knows the progress of the optimization.
  9. When the simulation ends, the timer is killed and the solution is displayed in a Message Box.
Observe los siguientes puntos claves en el programa:
  1. La codificación de la solución es directa, un valor de punto flotante es usado para x, y otro valor de punto flotante para inicializar y
  2. Un valor aleatorio fue usado para inicializar x y y.
  3. La solución fue perturbada al sumar un valor aleatorio a x y a y.
  4. Como éste es un problema de minimización, la propia función puede ser usada para evaluar la función. Así, es posible (en este caso) solamente evaluar la función para evaluar el error.
  5. La función SimAnnealCopy copia todas las variables que se usaron en la codificación, en este caso: x and y.
  6. Cuando el programa comienza ejecución, otra tarea (hilo) comienza a realizar la optimización. Así, el programa tiene dos hilos (threads).
  7. La ventana principal comienza un temporizador (timer) que ejecuta un bloque de código cada segundo.
  8. El temporizador es usado para mover información desde el hilo de optimización al hilo de la ventana principal, de tal forma que el usuario conoce el progreso de la optimización.
  9. Cuando la simulación termina, el temporizador es terminado y la solución se muestra en una caja de mensajes.

Tip
To design the error function, it is important to take into consideration all variables that need to be optimized. It is possible to use the summation, the product, the division, the exponential, etc., to combine all requirements and compute one single value. Negative error values are not allowed.
Para la diseñar la función de error se deben de tomar en consideración todos las variables a optimizar. Se puede sumar la suma, el producto, la división, exponenciales, etc., para combinar todos los requisitos y obtener un solo valor. Los valores negativos de error no son permitidos.

Tip
The Math::SimulatedAnnealing class implements the algorithm of Simulated Annealing. The SimulatedAnnealing::ThreadFunc function includes all the steps of SA.
La clase Math::SimulatedAnnealing implementa el algoritmo de templado simulado. La función SimulatedAnnealing::ThreadFunc incluye todos los pasos de SA.

Tip
The final temperature cannot be zero. However it can be close to zero, i.e., 0.001, 0.00001, etc.
La temperatura final no puede ser cero. Sin embargo se puede acercar a cero, por ejemplo: 0.001, 0.00001, etc.

Tip
You may find other functions to minimize at http://en.wikipedia.org/wiki/Test_functions_for_optimization
Usted puede encontrar otras funciones para minimizar en http://en.wikipedia.org/wiki/Test_functions_for_optimization

© Copyright 2000-2021 Wintempla selo. All Rights Reserved. Jul 22 2021. Home